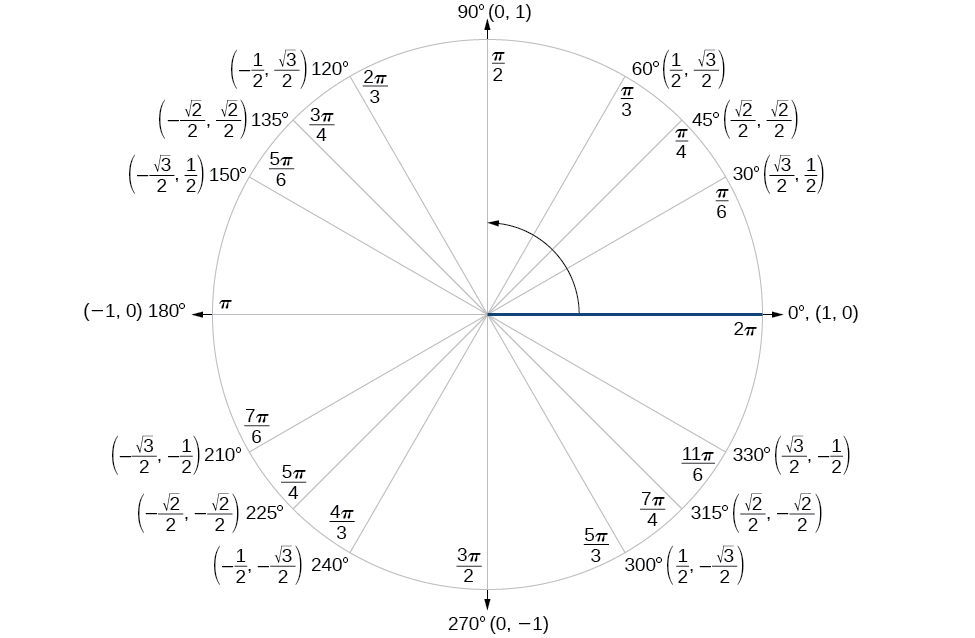
Unit Circle

• From advanced mathematics, you may remember the unit circle ¹. This will be important for this module.

  

Sum-Difference Identities

Cosine

$\cos(A\pm B)=\cos (A)\cos (B)\mp\sin (A)\sin (B)$

$\newcommand{\nl}[0]{}$

Proof for cosine sum-difference identity

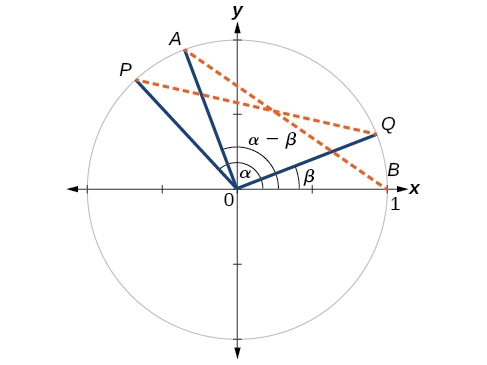
• Consider 2 points ($P$ and $Q$) on the unit circle:
  • Point $P$ is at an angle $\alpha$ from the positive x-axis with coordinates $(\sin (\alpha), \cos(\alpha))$
  • Point $Q$ is at an angle of $\beta$ from the positive x-axis, with coordinates $(\sin (\beta), \cos(\beta))$
• In this triangle, $\angle POQ$ will be $\alpha - \beta$

If this hard to visualise, a diagram is coming.

• Let’s make another triangle:
  • Point $A$ is located at an angle of $(\alpha-\beta)$ from the positive x-axis, and has coordinates $(\cos(\alpha-\beta),\sin(\alpha-\beta))$
  • Point $B$ is located at $(1,0)$
• If you’ve drawn out the 2 triangles, you will have noticed that $\triangle AOB$ and $\triangle POQ$ are rotations of each other, and are therefore congruent, so we can say that $PQ$ and $AB$ are equal

$$\text{Mathematically: }\triangle AOB\cong\triangle POQ,\therefore PQ=AB$$

• Now, we can find the distance from $P$ to $Q$ using the Cartesian distance formula: $$d_{PQ}= \sqrt{{(cos \alpha - cos \beta )}^2+{(sin \alpha - sin \beta )}^2}$$ $$= \sqrt{{\cos}^2 \alpha-2\cos \alpha \cos \beta+{\cos}^2 \beta+{\sin}^2 \alpha-2\sin \alpha \sin \beta+{\sin}^2 \beta}\qquad $$ $$\text {Apply Pythagorean identity and simplify.}$$ $$= \sqrt{({\cos}^2 \alpha+{\sin}^2 \alpha)+({\cos}^2 \beta+{\sin}^2 \beta)-2\cos \alpha \cos \beta-2\sin \alpha \sin \beta}$$ $$= \sqrt{1+1-2\cos \alpha \cos \beta-2\sin \alpha \sin \beta}$$ $$= \sqrt{2-2\cos \alpha \cos \beta-2\sin \alpha \sin \beta}\qquad$$ $$\text {Similarly, using the distance formula we can find the distance from A to B.}$$ $$d_{AB} = \sqrt{{(\cos(\alpha-\beta)-1)}^2+{(\sin(\alpha-\beta)-0)}^2}$$ $$= \sqrt{{\cos}^2(\alpha-\beta)-2\cos(\alpha-\beta)+1+{\sin}^2(\alpha-\beta)}\qquad$$ $$\text {Apply Pythagorean identity and simplify}$$ $$= \sqrt{({\cos}^2(\alpha-\beta)+{\sin}^2(\alpha-\beta))-2\cos(\alpha-\beta)+1}$$ $$= \sqrt{1-2\cos(\alpha-\beta)+1}$$ $$= \sqrt{2-2\cos(\alpha-\beta)}\qquad$$ $$\text {Subtract 2 from both sides and divide both sides by −2.}$$ $$\cos \alpha \cos \beta+\sin \alpha \sin \beta = \cos(\alpha-\beta)$$

Sine

$sin(A\pm B)=\sin A\cos B\pm \cos A \sin B$

Proof for sine sum-difference identity

• Substitute $90°-A$ for $A$ in the cosine sum-difference formula:
  • $\cos((90°-A)\pm B)=\cos(90°-A)\cos(B)\mp\sin(90°-A)\sin(B)$
  • $\text{Using }\sin(\theta)=\cos(90°-\theta), \cos(90°-(A\pm B))=\sin(A\pm B)$
  • $=\sin(A)\cos(B)\pm\cos(A)\sin(B)$
  • $\therefore\sin(A\pm B)=\sin(A)\cos(B)\pm\cos(A)\sin(B)$

Tangent

$\tan(A\pm B)=\frac{\sin(A\pm B)}{\cos(A\pm B)}=\frac{\tan(A)\pm \tan(B)}{1\mp\tan(A)tan(B)}$

Proof for tangent sum-difference identity

Honestly I’m not bothered to do it. I’ll probably get carpal tunnel syndrome from all these escape characters.

To prove it yourself, just use $tan\theta =\frac{sin\theta}{cos\theta},$ sub in the $\sin$ and $\cos$ identities, and simplify. It’s not that hard, its just tedious 😕.

- Jackson Taylor

Double Angle Identities

Sine

$\sin(2A)=2\sin(A)\cos(A)$

Proof

$sin(2A)=sin(A+A)$

$=sin A cos A + cos A sin A$

$=2 sin A cos A$

Cosine

$cos 2A=cos^2 A-sin^2 A$

Proof

$cos(2A)=cos(A+A)$

$=cos A cos A-sin A sin A$

$=cos^2 A-sin^2 A$

Tangent

$tan(2A)=\frac{2\tan(A)}{1-\tan^2 (A)}$

Proof

$\tan(2A)=\tan(A+A)$

$=\frac{\tan(A)+\tan(A)}{1-\tan(A)\tan(A)}$

$=\frac{2\tan(A)}{1-\tan^2 (A)}$

Product Identities

• These are just the sum-difference identities, rearranged to find the products of the ratios.

  This means I don’t have to do proofs! Yay!

  - Jackson Taylor

Cosine-Cosine

$cos(A)cos(B)=\frac{1}{2}[cos(A+B)+cos(A-B)]$

Sine-Sine

$sin(A)sin(B)=\frac{1}{2}[cos(A-B)+cos(A+B)]$

Sine-Cosine

$sin(A)cos(B)=\frac{1}{2}[sin(A+B)+sin(A-B)]$

Cosine-Sine

$cos(A)sin(B)=\frac{1}{2}[sin(A+B)-sin(A-B)]$

T-Formulae

$t=tan(\frac{A}{2})$

I’m not even bothered to type proofs anymore. Y’all can deal with screenshots.

- Jackson Taylor

• $sin A=\frac{2t}{1+t^2}$

  

• $cos A=\frac{1-t^2}{1+t^2}$

  

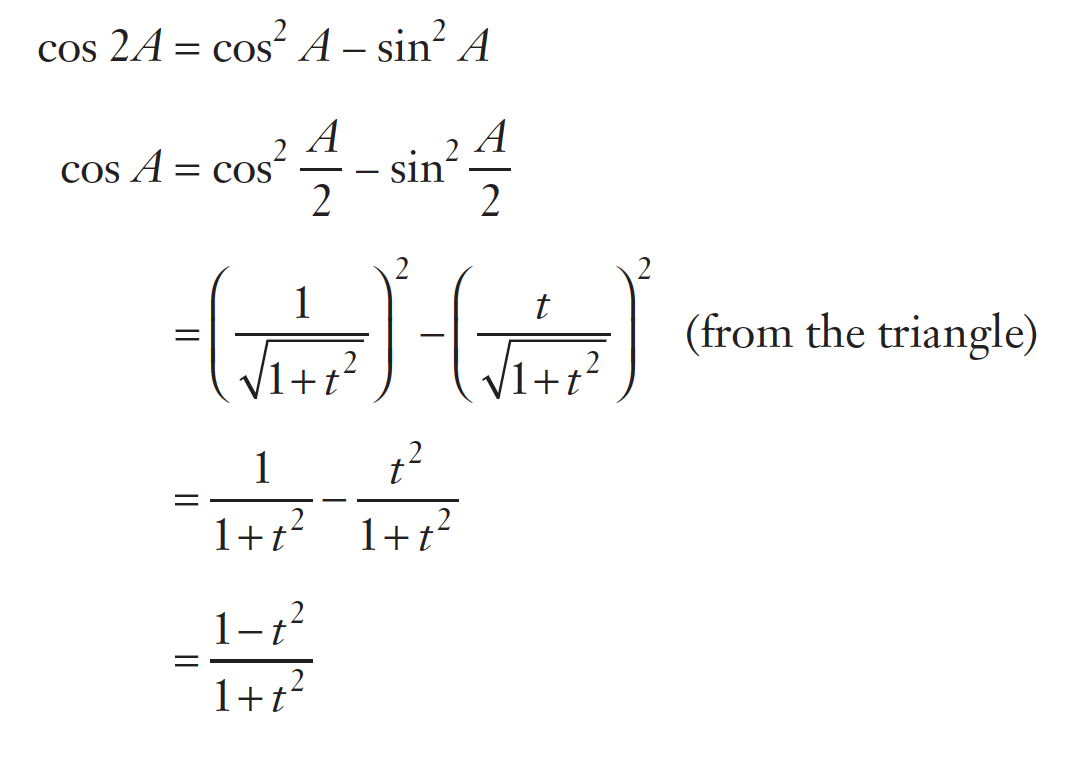
• $tan A=\frac{2t}{1-t^2}$

  

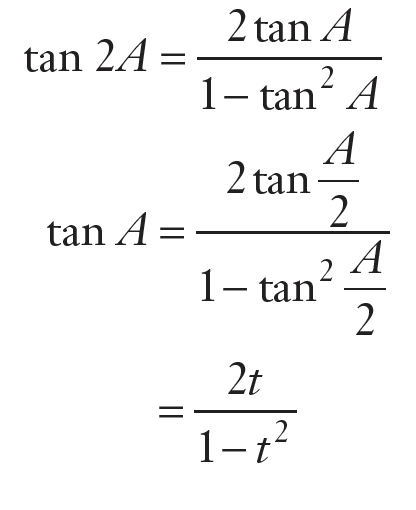
Inverse Trigonometric Functions

Notation

Inverse trigonometric functions are notated in one of 2 ways:

• The “arc” prefix:
  • $arcsin(x)$
  • $arccos(x)$
  • $arctan(x)$
  • $arcsec(x)$
  • $arccosec(x)/arccsc(x)$
  • $arccot(x)$
• The inverse $(^{-1})$ notation:
  • $sin^{-1}(x)$
  • $cos^{-1}(x)$
  • $tan^{-1}(x)$
  • $sec^{-1}(x)$
  • $cosec^{-1}(x)/csc^{-1}(x)$
  • $cot^{-1}(x)$

$y=\sin^{-1}(x)$

$y=\cos^{-1}(x)$

$y=\tan^{-1}(x)$

Properties

• $\sin^{-1}(-x)=-\sin^{-1}(x)$
• $cos^{−1}(−x)=\pi−cos^{−1}(x)$
• $tan^{−1}(−x)=−tan^{−1}(x)$
• $sin^{−1}(x)+cos^{−1}(x)=\frac{\pi}{2}$

And we’re done!

That’s all of Extension 1 Trigonometry (for year 11, anyway).

References