Module 3: Waves and Thermodynamics

Wave Properties

• Vibrating objects transfer energy through waves
• Waves are classified by what they move through
• There are two types: mechanical and electromagnetic

Mechanical Waves

• Mechanical waves transfer energy through vibrations in a medium
• Examples include water, sound and wind
• A wave can be a single pulse, or continuous

Waves only transfer energy from one point to another. THEY DO NOT TRANSFER MATTER! However, matter may move as the wave passes through it.

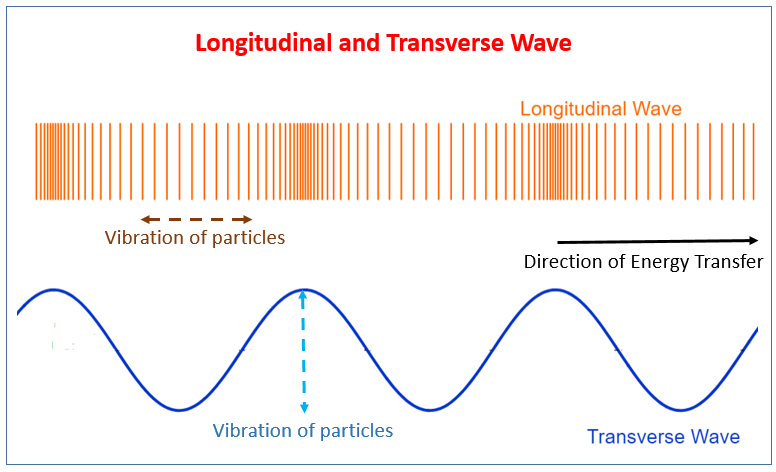
• Mechanical waves can be either transverse or longitudinal.

  • In a transverse wave, particles oscillate (move back and forth) perpendicular (at 90°) to the direction of energy transfer.

  • In a longitudinal wave, particles move parallel to the direction of energy transfer.

    

• This simulation demonstrates a wave - PHET COLORADO

Measuring Mechanical Waves

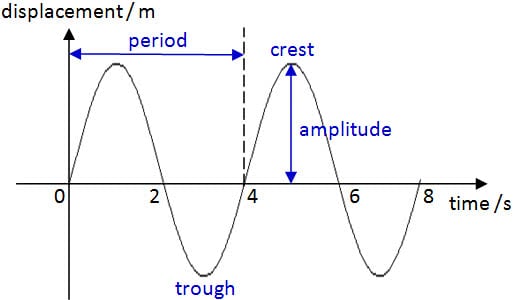
• Waves can be represented by displacement-distance graphs and displacement-time graphs.

• The graph takes a sinusoidal shape (like a sine wave)

The Role of the Medium

• Speed of sound waves in a medium depends on 2 main factors:

1. Elasticity of the medium
2. Density of the medium

• The more rigid a material is, the faster the mechanical waves are transmitted
• The more elastic a material is, the slower a mechanical wave is transmitted
• The higher the temperature a given medium is, the faster a mechanical wave will move through it.

Electromagnetic Waves

• All EM waves propagate through space at $3\times {10}^{8}m/s$
• EM waves do not require a medium as they self-propagate
• A charged particle produces an electric field.
• A moving charged particle produces a magnetic field.
• An oscillating charged particle produces an EM wave.
• EM waves consist of perpendicular electric and magnetic fields.

Other Properties of EM Waves

• All EM waves are transverse waves.

• All able to undergo:

  • Reflection
  • Refraction
  • Polarisation
  • Interference
  • Diffraction

• All EM waves travel in straight lines

Displacement-Time Graph of a Transverse Wave

• The displacement time graph of a transverse wave shows how a single particle is displaced from natural resting position as a function of time

Wave Behaviour

Wavefronts and Rays

• Rays refer to direction in which energy moves from initial disturbance which created the wave
• Wavefront essentially marks points at which energy of particles are equal

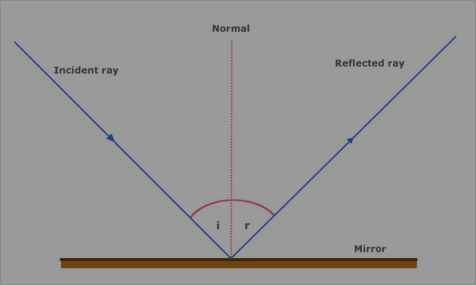
Reflection

• The law of reflection state that ${\theta }_i={\theta }_r$
• A reflected wave has the same frequency, wavelength, and speed as the incident (original) wave
• Wavefronts are identical before and after reflection

Convex Mirrors

• Rays diverge after reflection
• Used in car mirrors and surveillance systems

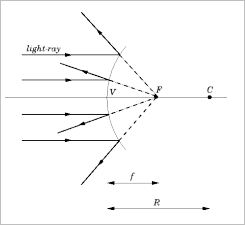
Concave Mirrors

• Curves inward and waves converge at the focus
• Used to reflect microwaves or radio waves from collecting dishes to receiving antenna

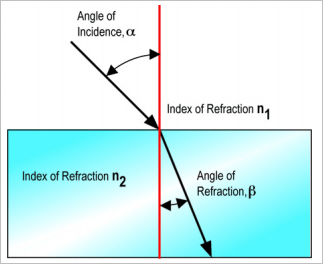
Refraction

• When an EM wave travels from one medium to another some of the wave will be absorbed, some reflected, and the rest propagates through the new medium

$$n_1\sin \left(\alpha \right)=n_2\sin \left(\beta \right)$$

• Where $\alpha$ and $\beta$ are the angles from the normal (the red line in the image) and n values are the refractive indices of the media
  • the refractive index of a material will usually be given in exams, but it is useful to remember that air is $n\approx 1,$ glass is $n\approx 1.5,$ and water is $n\approx \frac{4}{3}$
  • Usually, a more dense substance will have a higher refractive index

When light moves from one medium to another:

• Frequency of light remains unchanged
• Wavelength of light changes
• Velocity of wavelength changes
• When a wave slows down, it bends towards the normal

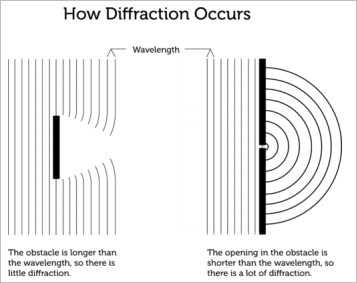
Diffraction

• Refers to the spreading if waves as the waves passes an object or travels through a gap between objects
• Wave diffracts around barrier at edges, leaving a shadow region behind it where the wave does not reach.
• The amount of diffraction is proportional to the wavelength AND the size of the slit:

$$\text{Diffraction}=\frac{\omega }{\lambda }$$

Superposition

• Superposition is the overlapping of two waves
• There are two types of superposition: constructive (waves add to make a larger wave) and destructive (waves cancel each other out to make a smaller wave)
• Superposition results in a temporary change of frequency, amplitude and phase
• Once the waves have passed each other, the superposition collapses, and both waves return to their original properties

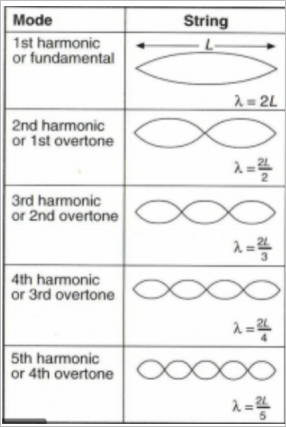
Standing Waves

• Standing waves are waves which do not appear to be moving along the medium

• Instead, the antinodes (peaks and troughs) seem to switch displacement twice every cycle

• Standing waves are frequently used in music, where:

$${\mathcal{f}}_n=n\cdot {\mathcal{f}}_1$$

$${\lambda }_n=\frac{1}{n}\cdot {\lambda }_1$$

• In other words, the frequency of harmonic n is equal to n multiplied by the frequency of harmonic 1 (usually middle C)

Resonance

• A phenomenon in which a vibrating system or external force drives another system to oscillate with greater amplitude at specific frequencies
• Occurs at frequencies where response amplitude is a maximum is termed “resonant frequency”

Sound Waves

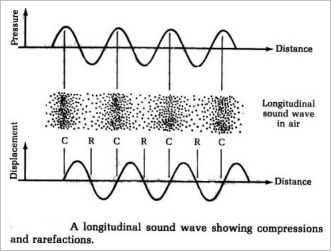
• Sound is a mechanical wave; the wave is caused by a vibrating source.
• Travel as alternating regions of compressions and rarefactions.
• Travel at 343m/s
• Changes depending on air pressure and temperature

• Sound waves are measured in $W/m^2$, and are calculated by:

$$I=\frac{P}{4\pi r^2}$$

Frequency and Pitch

• Frequency is the quantitative equivalent of pitch

Amplitude and Volume

• Amplitude and volume are directly proportional (increasing one increases the other)

Echoes:

• Minimum distance the boundary needs to be away (from both the source and the listener) is 17m.
• The sound wave has to travel a total of at least 34m.
• The best echoes come from hard, smooth surfaces.
• For a human to perceive two sounds as separate sounds, they MUST be 0.1 seconds apart.

The Doppler Effect

• When the source of a sound wave approaches an observer, the observer interprets the sound as compressed, and therefore higher pitched
• The opposite is true when the source is travelling away from an observer
• The frequency shift can be calculated by:

$$f\prime =f\left(\frac{v_{wave}+v_{observer}}{v_{wave}-v_{source}}\right)$$

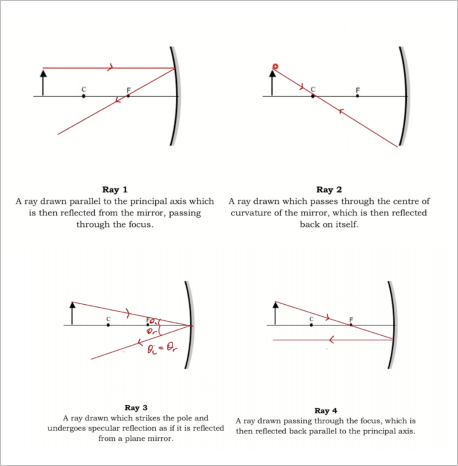
Ray Model of Light

Ray Diagrams

Describing Ray Diagrams

• Questions will often ask you to describe the image produced by a ray diagram

• To describe these images, use TOMP:

  • Type of image (real/virtual)
  • Orientation (upright/inverted)
  • Magnification (enlarged/diminished/true size)
  • Position (distance from the mirror)

• Magnification can be calculated by:

$$M=\frac{h_i}{h_o}\text{, where:}$$

• $M=$magnification scale
• $h_i=$ image height
• $h_o=$ object height

Mirror Formula

$$\frac{1}{f}=\frac{1}{u}+\frac{1}{v}\text{, where:}$$

• $f=$ focal length of the mirror (cm)

• $u=$ distance between mirror and object (cm)

• $v=$ distance between mirror and image (cm)

• Now that we have the mirror formula, we can expand the magnification formula:

$$M=\frac{h_i}{h_o}=\frac{-v}{u}$$

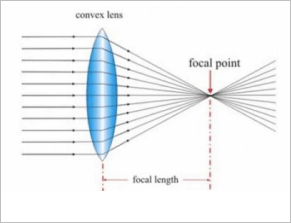
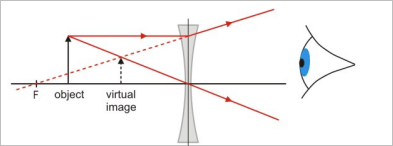
Lenses

• A lens is a transparent piece of material which bends light in a specific manner
• Converging lenses bend light rays to meet at a specific focal point
• Diverging lenses bend light away from each other

Converging Lens:

Diverging Lens:

Refractive Index

• The speed of a wave depends on the density of the medium

• The density, when referring to its effect on waves, is referred to as a medium’s refractive index

• A total vacuum has a refractive index of $n=1.00$

• A higher refractive index means light will travel slower in that medium

• Refractive index is calculated by:

$$n_{material}=\frac{c}{v_{material}}$$

• Where $c$ is the speed of light in a vacuum $(3\times {10}^8\text{ m/s})$

Thermodynamics

Temperature and Kinetic Energy

• While an object may be at rest, the particles it is composed of are in a constant state of motion
• As temperature increases, the Kinetic energy increases, so the particles move more quickly
• This allows energy to be transferred faster at higher temperatures

Heat is a measure of the transfer of thermal energy between bodies

Thermal Equilibrium

• Thermal energy is always transferred from regions of higher temperature to regions of lower temperature

• The Zeroth Law of thermodynamics states that:

  “If two thermodynamics systems are each in equilibrium with a third system, then they are also in equilibrium with each other.”

• The First Law of Thermodynamics, also known as the Law of Conservation of Energy, states that:

  “Energy cannot be created, nor destroyed.”

Specific Heat Capacity

• A measure of how much energy 1kg of a substance must absorb to increase in temperature by $1^{\circ }C$

• Water has a specific heat capacity of 4186J/kg/K

  • In other words, it takes 4186J of energy to increase the temperature of 1kg of water by 1 Kelvin

• Specific heat capacity can be calculated with the formula:

$$\mathrm{\Delta }Q=mc\mathrm{\Delta }T\text{, where:}$$

• $\mathrm{\Delta }Q=$change in energy (Joules)
• $m=$ mass of the substance (kg)
• $c=$ specific heat capacity of the substance (J/kg/K)
• $\mathrm{\Delta }T=$ change in temperature (K)

Latent Heat

• Latent heat of fusion is the amount of energy required to change 1kg of a substance from liquid to gas WITHOUT CHANGING ITS TEMPERATURE

$$Q=mL\text{, where:}$$

• $Q=$ Energy released (J)

• $m=$ mass of the substance (kg)

• $L=$ Latent heat of fusion (J/kg)